Các kết hợp trả lại
Sử dụng bảng số hoặc CTE tạo số, chọn từ 0 đến 2 ^ n - 1. Sử dụng các vị trí bit chứa 1s trong các số này để chỉ ra sự có mặt hoặc vắng mặt của các phần tử tương đối trong tổ hợp và loại bỏ những phần tử không có số lượng giá trị chính xác, bạn sẽ có thể trả về một tập hợp kết quả với tất cả các kết hợp mà bạn mong muốn.
WITH Nums (Num) AS (
SELECT Num
FROM Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
), Combos AS (
SELECT
ComboID = N.Num,
S.Value,
Cnt = Count(*) OVER (PARTITION BY N.Num)
FROM
Nums N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
)
SELECT
ComboID,
Value
FROM Combos
WHERE Cnt = @k
ORDER BY ComboID, Value;
Truy vấn này hoạt động khá tốt, nhưng tôi đã nghĩ ra cách để tối ưu hóa nó, lấy từ Đếm số bit song song Nifty để có được đúng số lượng mục được lấy tại một thời điểm. Điều này hoạt động nhanh hơn 3 đến 3,5 lần (cả CPU và thời gian):
WITH Nums AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM dbo.Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0f0f0f0f) + ((P2 / 16) & 0x0f0f0f0f)
FROM Nums2
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
)
SELECT
ComboID = N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
WHERE P3 % 255 = @k
ORDER BY ComboID, Value;
Tôi đã đọc và đọc trang đếm bit và nghĩ rằng điều này có thể hoạt động tốt hơn nếu tôi không thực hiện% 255 nhưng thực hiện tất cả các cách với số học bit. Khi có cơ hội, tôi sẽ thử nó và xem nó xếp chồng lên như thế nào.
Tuyên bố về hiệu suất của tôi dựa trên các truy vấn được chạy mà không có điều khoản ORDER BY. Để rõ ràng, những gì mã này đang làm là đếm số bit 1 được đặt trong Num từ Numbers bàn. Đó là bởi vì số đang được sử dụng như một loại chỉ mục để chọn các phần tử của tập hợp nằm trong tổ hợp hiện tại, vì vậy số bit 1 sẽ giống nhau.
Tôi hy vọng bạn thích nó!
Đối với bản ghi, kỹ thuật sử dụng mẫu bit của các số nguyên để chọn các thành viên của một tập hợp là những gì tôi đã đặt ra "Nối chéo theo chiều dọc". Nó dẫn đến việc kết hợp chéo nhiều bộ dữ liệu một cách hiệu quả, trong đó số lượng bộ &phép nối chéo là tùy ý. Ở đây, số bộ là số lượng mục được lấy tại một thời điểm.
Trên thực tế, kết hợp chéo theo nghĩa ngang thông thường (thêm nhiều cột vào danh sách cột hiện có với mỗi phép nối) sẽ trông giống như sau:
SELECT
A.Value,
B.Value,
C.Value
FROM
@Set A
CROSS JOIN @Set B
CROSS JOIN @Set C
WHERE
A.Value = 'A'
AND B.Value = 'B'
AND C.Value = 'C'
Các truy vấn của tôi ở trên có hiệu quả "tham gia chéo" nhiều lần nếu cần với chỉ một tham gia. Kết quả không được phân chia so với kết hợp chéo thực tế, nhưng đó là một vấn đề nhỏ.
Phê bình mã của bạn
Trước tiên, tôi có thể đề xuất thay đổi này đối với UDF giai thừa của bạn không:
ALTER FUNCTION dbo.Factorial (
@x bigint
)
RETURNS bigint
AS
BEGIN
IF @x <= 1 RETURN 1
RETURN @x * dbo.Factorial(@x - 1)
END
Giờ đây, bạn có thể tính toán các tập hợp lớn hơn nhiều, cộng với nó hiệu quả hơn. Bạn thậm chí có thể cân nhắc sử dụng decimal(38, 0) để cho phép các phép tính trung gian lớn hơn trong các phép tính kết hợp của bạn.
Thứ hai, truy vấn đã cho của bạn không trả về kết quả chính xác. Ví dụ:sử dụng dữ liệu thử nghiệm của tôi từ thử nghiệm hiệu suất bên dưới, tập hợp 1 giống như tập hợp 18. Có vẻ như truy vấn của bạn có một sọc trượt bao quanh:mỗi tập hợp luôn là 5 thành viên liền kề, trông giống như thế này (tôi xoay để dễ nhìn hơn):
1 ABCDE
2 ABCD Q
3 ABC PQ
4 AB OPQ
5 A NOPQ
6 MNOPQ
7 LMNOP
8 KLMNO
9 JKLMN
10 IJKLM
11 HIJKL
12 GHIJK
13 FGHIJ
14 EFGHI
15 DEFGH
16 CDEFG
17 BCDEF
18 ABCDE
19 ABCD Q
So sánh mẫu từ các truy vấn của tôi:
31 ABCDE
47 ABCD F
55 ABC EF
59 AB DEF
61 A CDEF
62 BCDEF
79 ABCD G
87 ABC E G
91 AB DE G
93 A CDE G
94 BCDE G
103 ABC FG
107 AB D FG
109 A CD FG
110 BCD FG
115 AB EFG
117 A C EFG
118 BC EFG
121 A DEFG
...
Chỉ để thúc đẩy mô hình bit -> chỉ mục kết hợp về nhà cho bất kỳ ai quan tâm, hãy lưu ý rằng 31 trong binary =11111 và mẫu là ABCDE. 121 trong hệ nhị phân là 1111001 và mẫu là A__DEFG (được ánh xạ ngược).
Kết quả hoạt động với bảng số thực
Tôi đã chạy một số thử nghiệm hiệu suất với các bộ lớn trên truy vấn thứ hai của tôi ở trên. Tôi không có bản ghi tại thời điểm này của phiên bản máy chủ được sử dụng. Đây là dữ liệu thử nghiệm của tôi:
DECLARE
@k int,
@n int;
DECLARE @set TABLE (value varchar(24));
INSERT @set VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q');
SET @n = @@RowCount;
SET @k = 5;
DECLARE @combinations bigint = dbo.Factorial(@n) / (dbo.Factorial(@k) * dbo.Factorial(@n - @k));
SELECT CAST(@combinations as varchar(max)) + ' combinations', MaxNumUsedFromNumbersTable = POWER(2, @n);
Peter đã chỉ ra rằng "phép nối chéo theo chiều dọc" này không hoạt động tốt như chỉ viết SQL động để thực sự thực hiện CROSS JOIN mà nó tránh. Với chi phí nhỏ của một vài lần đọc nữa, giải pháp của anh ấy có chỉ số tốt hơn từ 10 đến 17 lần. Hiệu suất truy vấn của anh ấy giảm nhanh hơn của tôi khi số lượng công việc tăng lên, nhưng không đủ nhanh để ngăn bất kỳ ai sử dụng nó.
Tập hợp số thứ hai bên dưới là hệ số được chia cho hàng đầu tiên trong bảng, chỉ để hiển thị tỷ lệ của nó.
Erik
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 7344 0 3861 8531 |
18•9 17141 0 7748 18536 | 2.3 2.0 2.2
20•10 76657 0 34078 84614 | 10.4 8.8 9.9
21•11 163859 0 73426 176969 | 22.3 19.0 20.7
21•20 142172 0 71198 154441 | 19.4 18.4 18.1
Peter
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 422 70 10263 794 |
18•9 6046 980 219180 11148 | 14.3 14.0 21.4 14.0
20•10 24422 4126 901172 46106 | 57.9 58.9 87.8 58.1
21•11 58266 8560 2295116 104210 | 138.1 122.3 223.6 131.3
21•20 51391 5 6291273 55169 | 121.8 0.1 613.0 69.5
Suy rộng ra, cuối cùng truy vấn của tôi sẽ rẻ hơn (mặc dù nó là từ đầu trong các lần đọc), nhưng không phải trong một thời gian dài. Để sử dụng 21 mục trong tập hợp đã yêu cầu một bảng số lên đến 2097152 ...
Đây là nhận xét mà tôi đã đưa ra ban đầu trước khi nhận ra rằng giải pháp của tôi sẽ hoạt động tốt hơn đáng kể với một bảng số nhanh:
Kết quả hoạt động với bảng số hiệu
Khi tôi viết câu trả lời này ban đầu, tôi đã nói:
Tôi đã thử nó và kết quả là nó hoạt động tốt hơn nhiều! Đây là truy vấn tôi đã sử dụng:
DECLARE @N int = 16, @K int = 12;
CREATE TABLE #Set (Value char(1) PRIMARY KEY CLUSTERED);
CREATE TABLE #Items (Num int);
INSERT #Items VALUES (@K);
INSERT #Set
SELECT TOP (@N) V
FROM
(VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q'),('R'),('S'),('T'),('U'),('V'),('W'),('X'),('Y'),('Z')) X (V);
GO
DECLARE
@N int = (SELECT Count(*) FROM #Set),
@K int = (SELECT TOP 1 Num FROM #Items);
DECLARE @combination int, @value char(1);
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM Nums
WHERE Num BETWEEN 0 AND Power(2, @N) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums1
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0F0F0F0F) + ((P2 / 16) & 0x0F0F0F0F)
FROM Nums2
), BaseSet AS (
SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM #Set
)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE P3 % 255 = @K;
Lưu ý rằng tôi đã chọn các giá trị thành các biến để giảm thời gian và bộ nhớ cần thiết để kiểm tra mọi thứ. Máy chủ vẫn thực hiện tất cả các công việc tương tự. Tôi đã sửa đổi phiên bản của Peter để tương tự và loại bỏ các tính năng bổ sung không cần thiết để cả hai đều gọn gàng nhất có thể. Phiên bản máy chủ được sử dụng cho các bài kiểm tra này là Microsoft SQL Server 2008 (RTM) - 10.0.1600.22 (Intel X86) Standard Edition on Windows NT 5.2 <X86> (Build 3790: Service Pack 2) (VM) chạy trên máy ảo.
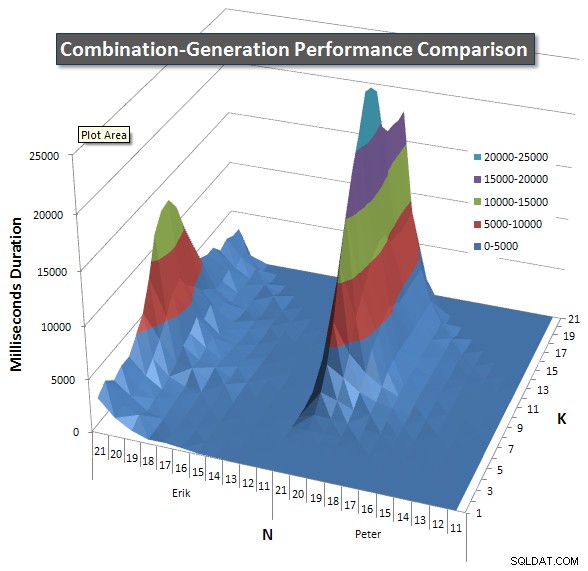
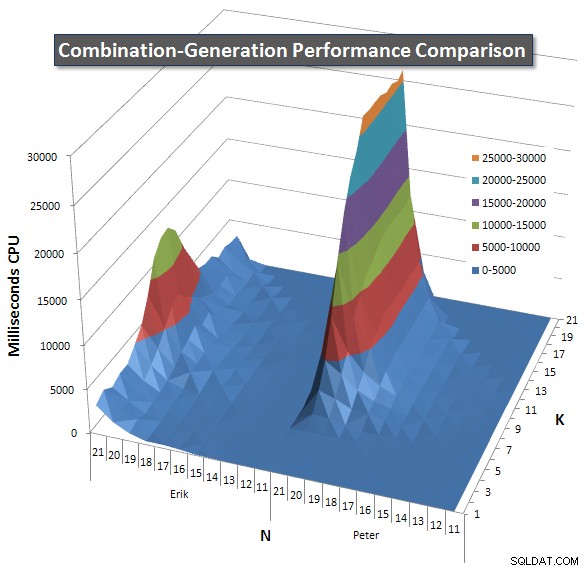
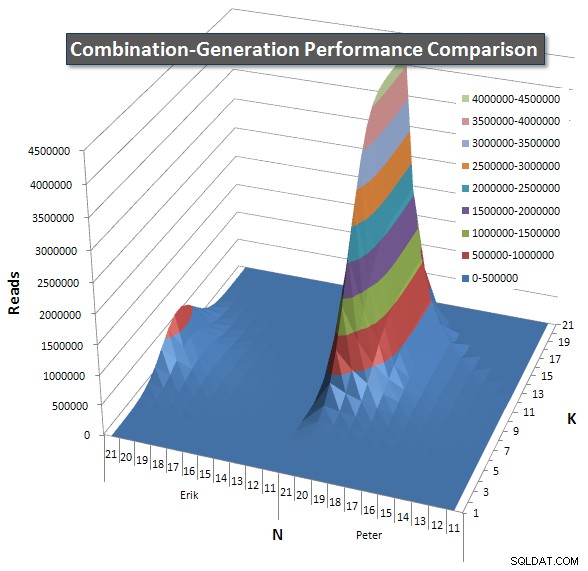
Dưới đây là biểu đồ hiển thị đường cong hiệu suất cho các giá trị của N và K lên đến 21. Dữ liệu cơ sở cho chúng nằm trong một câu trả lời khác trên trang này . Các giá trị là kết quả của 5 lần chạy của mỗi truy vấn ở mỗi giá trị K và N, tiếp theo là loại bỏ các giá trị tốt nhất và kém nhất cho mỗi chỉ số và lấy trung bình 3 giá trị còn lại.
Về cơ bản, phiên bản của tôi có "vai" (ở góc ngoài cùng bên trái của biểu đồ) ở giá trị cao của N và giá trị thấp của K khiến nó hoạt động kém hơn ở đó so với phiên bản SQL động. Tuy nhiên, điều này vẫn khá thấp và không đổi, và đỉnh trung tâm xung quanh N =21 và K =11 đối với Thời lượng, CPU và Số lần đọc thấp hơn nhiều so với phiên bản SQL động.
Tôi đã bao gồm một biểu đồ về số hàng mà mỗi mục dự kiến sẽ trả về để bạn có thể thấy cách truy vấn thực hiện xếp chồng lên nhau so với mức độ lớn của công việc mà nó phải thực hiện.
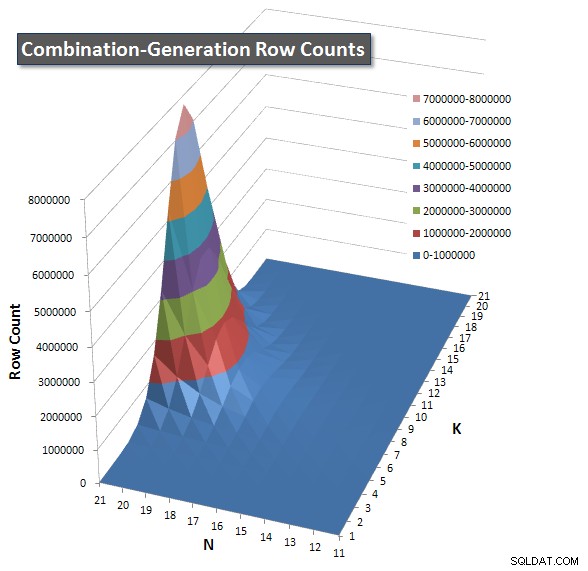
Vui lòng xem câu trả lời bổ sung của tôi trên trang này để có kết quả hoạt động hoàn chỉnh. Tôi đã đạt đến giới hạn ký tự của bài đăng và không thể đưa nó vào đây. (Bất kỳ ý tưởng nào khác để đặt nó?) Để đưa mọi thứ vào quan điểm so với kết quả hoạt động của phiên bản đầu tiên của tôi, đây là định dạng giống như trước đây:
Erik
Các mụcItems CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 354 378 12382 0 |
18•9 1849 1893 97246 0 | 5.2 5.0 7.9
20•10 7119 7357 369518 0 | 20.1 19.5 29.8
21•11 13531 13807 705438 0 | 38.2 36.5 57.0
21•20 3234 3295 48 0 | 9.1 8.7 0.0
Peter
Các mụcItems CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 41 45 6433 0 |
18•9 2051 1522 214021 0 | 50.0 33.8 33.3
20•10 8271 6685 864455 0 | 201.7 148.6 134.4
21•11 18823 15502 2097909 0 | 459.1 344.5 326.1
21•20 25688 17653 4195863 0 | 626.5 392.3 652.2
Kết luận
- Các bảng số trực tuyến tốt hơn một bảng thực có chứa các hàng, vì việc đọc một bảng ở số lượng hàng lớn đòi hỏi rất nhiều I / O. Tốt hơn là sử dụng một CPU nhỏ.
- Các thử nghiệm ban đầu của tôi không đủ rộng để thực sự hiển thị các đặc điểm hiệu suất của hai phiên bản.
- Phiên bản của Peter có thể được cải thiện bằng cách làm cho mỗi JOIN không chỉ lớn hơn mục trước mà còn hạn chế giá trị tối đa dựa trên số lượng mục khác phải phù hợp với tập hợp. Ví dụ:tại 21 mục được lấy 21 hàng tại một thời điểm, chỉ có một câu trả lời trong số 21 hàng (tất cả 21 mục, một lần), nhưng các bộ hàng trung gian trong phiên bản SQL động, ở đầu kế hoạch thực thi, chứa các kết hợp chẳng hạn như " AU "ở bước 2 mặc dù giá trị này sẽ bị loại bỏ ở lần nối tiếp theo vì không có giá trị nào cao hơn" U ". Tương tự, một tập hợp hàng trung gian ở bước 5 sẽ chứa "ARSTU" nhưng kết hợp hợp lệ duy nhất tại thời điểm này là "ABCDE". Phiên bản cải tiến này sẽ không có đỉnh thấp hơn ở trung tâm, vì vậy có thể không cải thiện nó đủ để trở thành người chiến thắng rõ ràng, nhưng ít nhất nó sẽ trở nên đối xứng để các biểu đồ không ở mức tối đa quá giữa khu vực mà sẽ tụt lại về gần 0 như phiên bản của tôi (xem góc trên cùng của các đỉnh cho mỗi truy vấn).
Phân tích thời lượng
- Không có sự khác biệt thực sự đáng kể giữa các phiên bản về thời lượng (> 100 mili giây) cho đến khi 14 mục được lấy 12 mục cùng một lúc. Tính đến thời điểm này, phiên bản của tôi thắng 30 lần và phiên bản SQL động thắng 43 lần.
- Bắt đầu từ 14 • 12, phiên bản của tôi nhanh hơn 65 lần (59> 100ms), phiên bản SQL động 64 lần (60> 100ms). Tuy nhiên, tất cả các lần phiên bản của tôi đều nhanh hơn, nó tiết kiệm được tổng thời lượng trung bình là 256,5 giây và khi phiên bản SQL động nhanh hơn, nó tiết kiệm được 80,2 giây.
- Tổng thời lượng trung bình cho tất cả các thử nghiệm là Erik 270,3 giây, Peter 446,2 giây.
- Nếu một bảng tra cứu được tạo để xác định phiên bản nào sẽ sử dụng (chọn phiên bản nhanh hơn cho các đầu vào), tất cả các kết quả có thể được thực hiện trong 188,7 giây. Mỗi lần sử dụng chế độ chậm nhất sẽ mất 527,7 giây.
Phân tích lượt đọc
Phân tích thời lượng cho thấy truy vấn của tôi chiến thắng với số tiền đáng kể nhưng không quá lớn. Khi số liệu được chuyển sang số lần đọc, một bức tranh rất khác sẽ xuất hiện - truy vấn của tôi sử dụng trung bình 1/10 số lần đọc.
- Không có sự khác biệt thực sự đáng kể giữa các phiên bản về số lần đọc (> 1000) cho đến khi 9 mục được lấy 9 mục cùng một lúc. Tính đến thời điểm này, phiên bản của tôi thắng 30 lần và phiên bản SQL động thắng 17 lần.
- Bắt đầu từ 9 • 9, phiên bản của tôi sử dụng ít lần đọc hơn 118 lần (113> 1000), phiên bản SQL động 69 lần (31> 1000). Tuy nhiên, tất cả những lần phiên bản của tôi sử dụng ít lần đọc hơn, nó đã tiết kiệm được tổng cộng trung bình 75,9 triệu lần đọc và khi phiên bản SQL động nhanh hơn, nó đã tiết kiệm được 380 nghìn lần đọc.
- Tổng số lần đọc trung bình cho tất cả các thử nghiệm là Erik 8,4 triệu, Peter 84 triệu.
- Nếu một bảng tra cứu được tạo để xác định phiên bản nào sẽ sử dụng (chọn phiên bản tốt nhất cho các đầu vào), tất cả các kết quả có thể được thực hiện trong 8 triệu lần đọc. Mỗi lần sử dụng câu tệ nhất sẽ mất 84,3 triệu lượt đọc.
Tôi rất muốn xem kết quả của một phiên bản SQL động được cập nhật đặt giới hạn trên bổ sung cho các mục được chọn ở mỗi bước như tôi đã mô tả ở trên.
Phụ lục
Phiên bản sau của truy vấn của tôi đạt được sự cải thiện khoảng 2,25% so với kết quả hiệu suất được liệt kê ở trên. Tôi đã sử dụng phương pháp đếm bit HAKMEM của MIT và thêm Convert(int) trên kết quả của row_number() vì nó trả về một bigint. Tất nhiên, tôi ước đây là phiên bản tôi đã sử dụng cho tất cả các thử nghiệm hiệu suất cũng như biểu đồ và dữ liệu ở trên, nhưng không chắc tôi sẽ làm lại nó vì nó tốn nhiều công sức.
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Convert(int, Num) Num
FROM Nums
WHERE Num BETWEEN 1 AND Power(2, @N) - 1
), Nums2 AS (
SELECT
Num,
P1 = Num - ((Num / 2) & 0xDB6DB6DB) - ((Num / 4) & 0x49249249)
FROM Nums1
),
Nums3 AS (SELECT Num, Bits = ((P1 + P1 / 8) & 0xC71C71C7) % 63 FROM Nums2),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM #Set)
SELECT
N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
Bits = @K
Và tôi không thể cưỡng lại việc hiển thị thêm một phiên bản có tính năng tra cứu để có được số lượng bit. Nó thậm chí có thể nhanh hơn các phiên bản khác:
DECLARE @BitCounts binary(255) =
0x01010201020203010202030203030401020203020303040203030403040405
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0304040504050506040505060506060704050506050606070506060706070708;
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (SELECT Convert(int, Num) Num FROM Nums WHERE Num BETWEEN 1 AND Power(2, @N) - 1),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM ComboSet)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums1 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
@K =
Convert(int, Substring(@BitCounts, N.Num & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 256 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 65536 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 16777216, 1))