Mọi người thường nói rằng lập chỉ mục là một kỹ thuật cần thiết để xử lý các truy vấn hiệu quả trong trường hợp cơ sở dữ liệu của bạn đủ lớn. Bài đăng này là để tóm tắt chỉ mục cơ sở dữ liệu là gì và xem lại hash và B + Tree.
Chỉ mục là một cấu trúc dữ liệu tổ chức các bản ghi để tối ưu hóa các loại hoạt động truy xuất nhất định. Chúng tôi có thể tạo chỉ mục trên một trường của bảng sau đó truy xuất tất cả các bản ghi đáp ứng các điều kiện tìm kiếm trên search-key đồng ruộng. Nếu không có chỉ mục, truy vấn của chúng tôi sẽ kết thúc quét tuyến tính toàn bộ nội dung của bảng để chỉ tìm nạp một hoặc một vài bản ghi.
Trong bài đăng này, tôi muốn tóm tắt hiệu suất và các trường hợp sử dụng của hai kỹ thuật lập chỉ mục phổ biến: Chỉ mục băm và B + cây
Chỉ mục băm
Kỹ thuật này được sử dụng rộng rãi để tạo chỉ mục trong bộ nhớ chính vì tính chất thu hồi nhanh của nó. Nó có độ phức tạp hoạt động trung bình O (1) và độ phức tạp lưu trữ O (n).
Trong nhiều sách, người ta sử dụng thuật ngữ bucket để biểu thị một đơn vị lưu trữ lưu trữ một hoặc nhiều bản ghi
Có hai điều cần thảo luận khi nói đến băm:
- Hàm băm:ánh xạ các khóa tìm kiếm (làm đầu vào của nó) thành một số nguyên đại diện cho khóa đó trong nhóm.
- Lược đồ băm:cách đối phó với xung đột khóa sau khi băm.

Có người hỏi:tại sao lại va chạm? Một hàm băm hoàn hảo có bao giờ tồn tại không? Trên thực tế, giả sử các khóa của bạn là một tập hợp vô hạn, không thể ánh xạ chúng thành một tập hợp các số nguyên 32 bit mà không có va chạm. Cần có sự cân bằng giữa tính toán và tỷ lệ va chạm.
Có một vài lược đồ băm đáng được đề cập:thăm dò tuyến tính, băm chuỗi và băm mở rộng. Các thuật toán tra cứu / chèn / xóa thay đổi tùy theo lược đồ băm, ví dụ:băm chuỗi giải quyết các xung đột chính bằng cách đặt các phần tử có cùng giá trị băm trong cùng một nhóm.
Ưu điểm
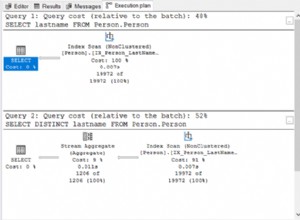
- Chỉ mục băm thích hợp cho việc tra cứu bình đẳng hoặc khóa chính. Các truy vấn có thể được hưởng lợi từ chỉ số băm để nhận được phân bổ chi phí tra cứu O (1). Ví dụ:
SELECT name, id FROM student WHERE id = '1315';
Nhược điểm
Bảng băm có một số hạn chế:
- Truy vấn phạm vi không hiệu quả. Bảng băm dựa trên phân phối đồng đều. Nói cách khác, bạn không có quyền kiểm soát nơi sắp đặt mục nhập chỉ mục.
- Khả năng mở rộng thấp:hiệu suất của hoạt động tra cứu có thể suy giảm khi có nhiều va chạm và nó yêu cầu thay đổi kích thước bảng băm sau đó chia sẻ lại các mục nhập chỉ mục hiện có.
B + Cây
Đây là một cấu trúc dữ liệu cây tự cân bằng giữ cho dữ liệu theo thứ tự được sắp xếp và cho phép tìm kiếm nhanh trong mỗi nút, thường sử dụng tìm kiếm nhị phân.
B + Tree là một triển khai chỉ mục tiêu chuẩn trong hầu hết các hệ thống cơ sở dữ liệu quan hệ.
B + Tree về cơ bản là một cây tìm kiếm M-way có cấu trúc như sau:
- cân bằng hoàn toàn:các nút lá luôn có cùng chiều cao.
- mọi nút bên trong không phải nút gốc đều đầy ít nhất một nửa (M / 2 - 1 <=số khóa <=M - 1).
- mọi nút bên trong có k khóa đều có k + 1 nút con không rỗng.
Mỗi nút của cây có một mảng các cặp khóa-giá trị đã được sắp xếp. Cặp khóa-giá trị được xây dựng từ (giá trị khóa-tìm kiếm, con trỏ) cho các nút gốc và nút bên trong. Giá trị nút lá có thể có 2 khả năng:
- bản ghi thực tế
- con trỏ tới bản ghi thực tế
Tra cứu giá trị v
- Bắt đầu với nút gốc
- Mặc dù nút không phải là nút lá, chúng tôi thực hiện:
- Tìm Ki nhỏ nhất trong đó Ki> =v
- If Ki ==v:đặt nút hiện tại thành nút được trỏ bởi Pi + 1
- Nếu không, hãy đặt nút hiện tại thành nút được trỏ bởi Pi

Các khóa trùng lặp
Nói chung, khóa tìm kiếm có thể bị trùng lặp, để giải quyết vấn đề này, hầu hết các triển khai cơ sở dữ liệu đều sử dụng khóa tìm kiếm tổng hợp. Ví dụ:chúng tôi muốn tạo một chỉ mục trên student_name thì khóa tìm kiếm tổng hợp của chúng ta phải là (student_name, Ap) trong đó Ap là khóa chính của bảng.
Ưu điểm
Có hai tính năng chính mà B + tree cung cấp:
- Giảm thiểu các hoạt động I / O
- Giảm chiều cao:B + Cây có hệ số phân cành khá lớn (giá trị từ 50 đến 2000 thường sử dụng) làm cho cây mập, lùn. Hình bên dưới minh họa một cây B + có chiều cao là 2. Như chúng ta có thể thấy các nút được trải rộng, cần ít nút hơn để đi xuống một lá. Chi phí tìm kiếm một giá trị duy nhất là chiều cao của cây + 1 để truy cập ngẫu nhiên vào bảng.
- Khả năng mở rộng:
- Bạn có hiệu suất có thể dự đoán được cho tất cả các trường hợp, cụ thể là O (log (n)). Đối với cơ sở dữ liệu, điều đó thường quan trọng hơn việc có hiệu suất trường hợp trung bình hoặc tốt hơn.
- Cây luôn duy trì trạng thái cân bằng khi thực hiện. A B + Cây có n khóa luôn có độ sâu là O (log (n)). Do đó, hiệu suất sẽ không suy giảm nếu cơ sở dữ liệu phát triển lớn hơn. Cây bốn cấp có hệ số phân nhánh là 500 có thể lưu trữ tối đa 256 TB với điều kiện trang đó có kích thước 4KB.

- B + Tree phù hợp nhất cho các truy vấn phạm vi, ví dụ:
"SELECT * FROM student WHERE age > 20 AND age < 22"
Kết luận
Mặc dù chỉ mục băm hoạt động tốt hơn về các truy vấn đối sánh chính xác, B + Tree được cho là cấu trúc chỉ mục được sử dụng rộng rãi nhất trong RDBMS nhờ hiệu suất nhất quán về tổng thể và khả năng mở rộng cao.
| B + Cây | Hash | |
|---|---|---|
| Thời gian tra cứu | O (log (n)) | O (log (1)) |
| Thời gian chèn | O (log (n)) | O (log (1)) |
| Thời gian xóa | O (log (n)) | O (log (1)) |
Gần đây, cây hợp nhất có cấu trúc nhật ký (LSM-tree) đã thu hút sự quan tâm đáng kể như một đối thủ của B + -tree, vì cấu trúc dữ liệu của nó có thể cho phép sử dụng không gian lưu trữ hiệu quả hơn. Tôi sẽ nghiên cứu kỹ hơn và đăng bài về nó trong tương lai gần.